今天是白色情人节吗?是。
但今天也是“π日”。
我不知道,有多少人像我一样,从小就很纳闷——π这玩意儿,到底咋算出来的。
有人也许会说,这还不简单,圆周率嘛,圆周长和直径的比啊,这都不知道?不知道查百度啊,你这学怎么上的......
我不是这个意思。
我的意思是说,大家都知道,π是“无理数”,也叫“无限不循环小数”。翻译成人话,就是小数点之后永远没有尽头——因为不是两个整数之比。
现在,小数点后面已经算到60万亿位了。
可对于人力来说,甭说60万亿位,六位也能算死了吧?那这60万亿位到底咋出来的呢?
01 祖冲之的疑惑
一提圆周率,老外想到的首先是阿基米德,中国人首先想到的是祖冲之。
就算你数学不咋地,但学过历史,你也应该知道,公元5世纪,有个叫祖冲之的县长,把圆周率算到了“3.1415926与3.1415927之间”这么一个狭小的范围。
对于南北朝时代的人来说,这太炸裂了,对不?
不过,世界知道有祖冲之这么一号,倒不是因为这个演算结果。
据说,当年苏联的“月球3号”探测器,发现了一批月球上的陨石坑,想要用一批各个国家的科学名人来命名,就挨个儿给各国打电话:“你们那儿有什么牛X科学家?我们打算拿来给月球上的大坑命名。”
问到我们国家的时候,提到了祖冲之。在这之前,谁叫祖冲之,他是干嘛的,压根儿没人知道。
其实,祖冲之要算圆周率,并不是出于对数学的爱好,而是为了研究历法。他研究出了《大明历》(跟明朝没有关系),提出了在391年插入144个闰月的新玩法,并且首次引入了“岁差”的概念。
祖冲之的家庭,在那个崇尚门阀的时代,算不上啥大官。他的爷爷是刘宋朝的“大匠卿”,管土木工程的。具体出身是什么情况,咱就不讲了,您自行百度百科。

他研究圆周率的方法,也不是他自己发明的,而是早就有。古书上说“径一周三”,认为圆周率就是3,不过这等于没说——傻子拿一张大饼,把饼边儿都撕下来排成一条,也知道差不多是大饼直径的三倍。
这个世界上,不信邪的人总是很多,研究这个数,成了很多数学家的心结。到了东汉,张衡算的圆周率是3.162,魏晋的数学家刘徽又算出3.1416。
这就完了么?远远不够。历法这东西,总是越精密越好——因为地球太阳月亮还有它们的运行轨道很烦人,转来转去,总有误差。这种误差,一年两年你还看不出来,一旦时间的力量长久加持,这误差就太吓人了,到最后大夏天刮西北风,大冬天穿比基尼,这日子就甭过了。
祖冲之决定把圆周率继续算下去,但用的方法,还是刘徽记载过的“割圆法”。说白了,就是不断倍增圆内接正多边形的边数,从内接六边形开始,一直无限倍增。
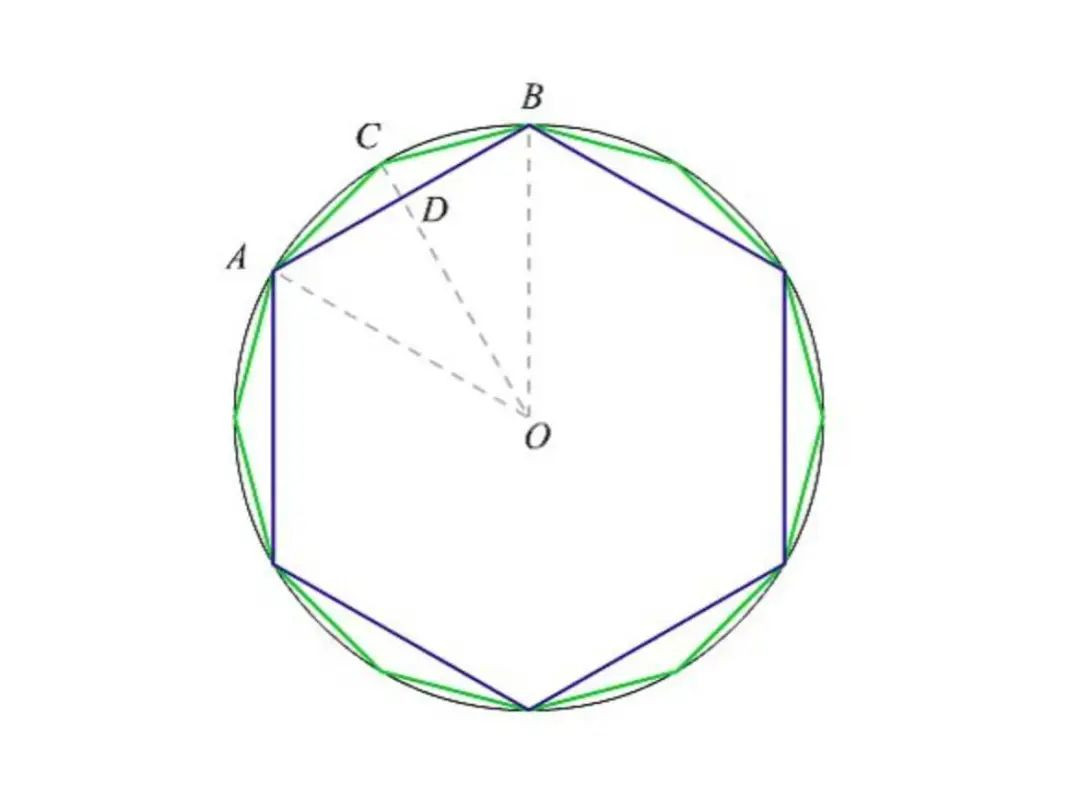
这叫什么?这其实就叫微积分,只不过当时古人没有这个概念罢了。
祖冲之怎么算π的,在《隋书·律历志》有很详细的记载:
“宋末,南徐州从事史祖冲之,更开密法,以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。”
不过,这种“割圆法”还可以继续穷尽下去,到1610年,德国人算到了小数点以后35位。
祖冲之老先生的结果一直领先了800年,祖先生威武。
02 牛顿的公式
不过,虽然“割圆法”在理论上可以无限制地分下去,但理论毕竟是理论。真算到一定程度,就来到了人力穷尽的边界。据说16世纪晚期,法国有个哥们儿,算过内接圆的正393216边形。17世纪的时候,这个记录又被荷兰人打破,算了一个“正2的62次方”边形。
咔,想想都惊悚。
很显然,要想继续把这玩意儿算下去,就需要其他方法,不然真会死人的。
1666年,有个英国小伙子叫牛顿,因为躲黑死病在家隔离。隔离,对咱们很多人来说都不陌生了,这也干不了,那也干不了。
干嘛去呢?算数玩儿吧!
这个期间,苹果砸牛顿脑袋上其实倒不一定发生过,但他闲的没事算了很多简单式倒是真的——比如(1+x)2。
这个东西展开,就=(1+x)(1+x)=1+2X+X2
以此类推,(1+X)3=(1+x)(1+2x+x2)=1+3X+3X2+X3
再往下,自己算去吧,公众号里写这玩意儿太累了。总之就是(1+X)n
如果你只看X乘方的系数,你就会发现,这就是一个“帕斯卡三角”
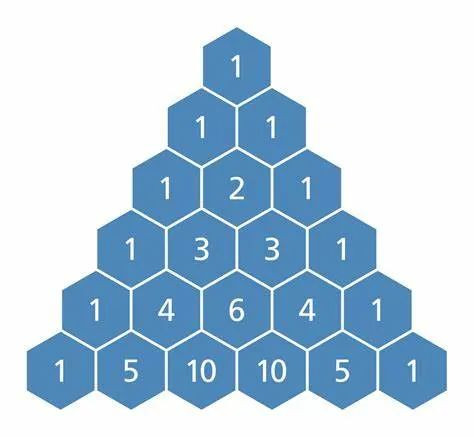
牛顿就想,如果(1+X)n的n不是正整数呢?比如是负数呢?有限项一下就变成无限项了,也就是无穷级数。
如果(1+X)n的n居然连负数都不是了呢?是分数了呢?
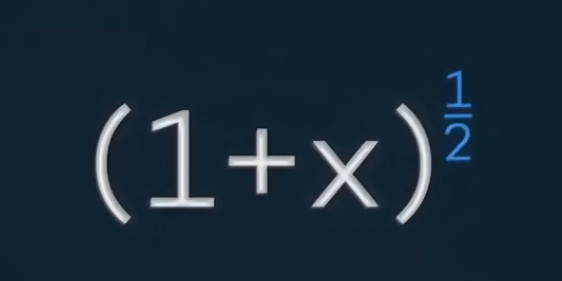
好玩的事就来了。因为圆的方程,恰好是X2+Y2=1
所以呢?
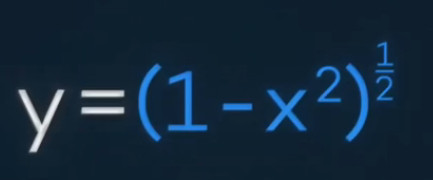
这就跟上面的那个式子完全一样了嘛,无非是把“X”替换成“-X2”就好了。
最后呢?设我们说的圆是个“单位圆”——也就是平面直角坐标系上,圆心为原点,半径为1的圆。将曲线在[0,1]这一段来个积分,你就得到了1/4个圆的面积,又因为你知道圆形的面积公式是S=π*R的平方
于是一顿折腾后,你就得到了这个——
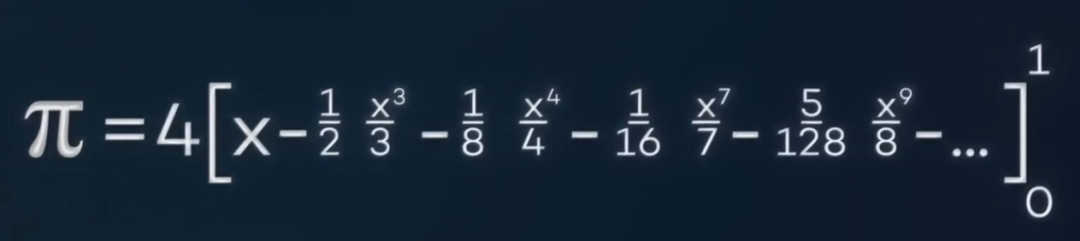
但是这东西收敛得太慢了,能不能收敛快一点呢?
于是又一顿折腾后,不再算1/4个圆,改成只算1/4圆里的一部分,式子就变成了这样——
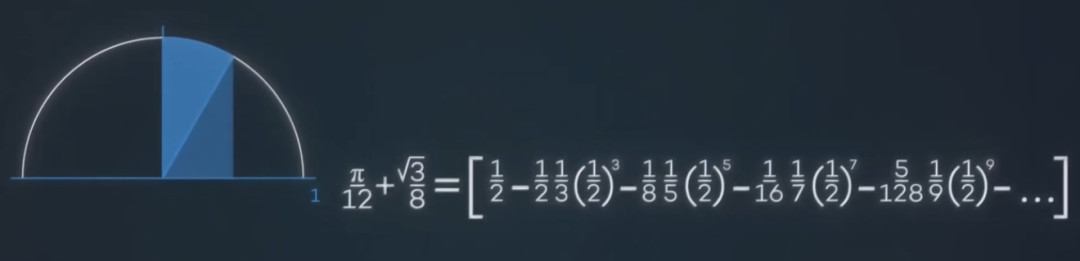
并最终得到了这个——
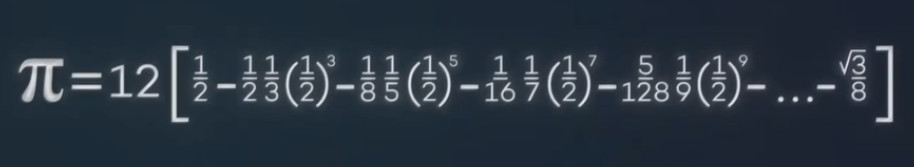
要实现上文说到过的“正2的62次方”边形的计算精度,你只需要照着这个公式算50位就行了。
所以我们知道了,之所以π如今能够算到小数点之后60万亿位,真不是不断“割圆”算出来的。
03 科学的力量
无可否认,祖冲之老爷子的成就巨大。独领世界风骚800年,泰山不是堆的,牛逼不是吹的。
但我们也不可否认,与牛顿(无穷级数的算法发明人,其实还有其他说法)的公式比起来,祖老爷子的辉煌成就,则完全是另一个路数。(当然,我们也说了,祖老爷子的初衷就不是为了研究算法,而是为了研究历法)
我们平常总说“科技科技”,但科技与科技之间,差别也蛮大。
有一种科技,意味着捏沙成团,无中生有,发前人所未发,想前人所未想,在没有路的地方走出路来。
另一种科技,是将已经有的路拓宽、拓深,做到无人能极的极致。
两种科技,都足够赢得世人的尊敬。但我们要看到,第二种科技,经常成为第一种科技的附庸,沦为低附加值的附属品,尽管你足够努力、足够拼搏,也总是在别人打开的路上走路,到哪年哪月,也是要交过路费的。
那么,怎办哩?
这么说吧,祖冲之老爷子的家庭出身,我们已经说了,《大明历》,说白了是进献给皇帝用的一种规矩天下的工具。
而牛顿小时候就死了爹,成天威胁要把继父和母亲一起烧掉,小时候是个标准的问题少年,成绩一般,但什么都爱玩,对化学、数学、神学都同时爱的发疯,晚年甚至还沉迷在炼金术里。
让孩子当“好学生”交论文,还是让孩子神神叨叨玩科学,不一定是答案,但可能有点启发。
最后说一句,如果“牛顿公式”的推倒过程你没看懂,就自己上网去查吧,反正我这水平也就解释到这儿了。

